Řešení systému rovnic v aplikaci Microsoft Excel

Schopnost řešit systémy rovnic může často být prospěšná nejen učení, ale i v praxi. Současně ne každý uživatel PC ví, že existují vlastní varianty řešení lineárních rovnic v aplikaci Excel. Zjistěte, jak tento úkol provádět různými způsoby pomocí různých nástrojů tohoto stolního procesoru.

Řešení

Každá rovnice může být považována za vyřešené pouze tehdy, když její kořeny jsou nalezeny. V aplikaci Excel existuje několik možností pro nalezení kořenů. Podívejme se na každou z nich.

Metoda 1: Metoda matice

Nejběžnějším způsobem, jak vyřešit systém lineárních rovnic s nástroji aplikace Excel, je použít maticovou metodu. Skládá se z konstrukce matice koeficientů výrazů a pak z vytváření inverzní matice. Pokusme se použít tuto metodu k vyřešení následujícího systému rovnic:


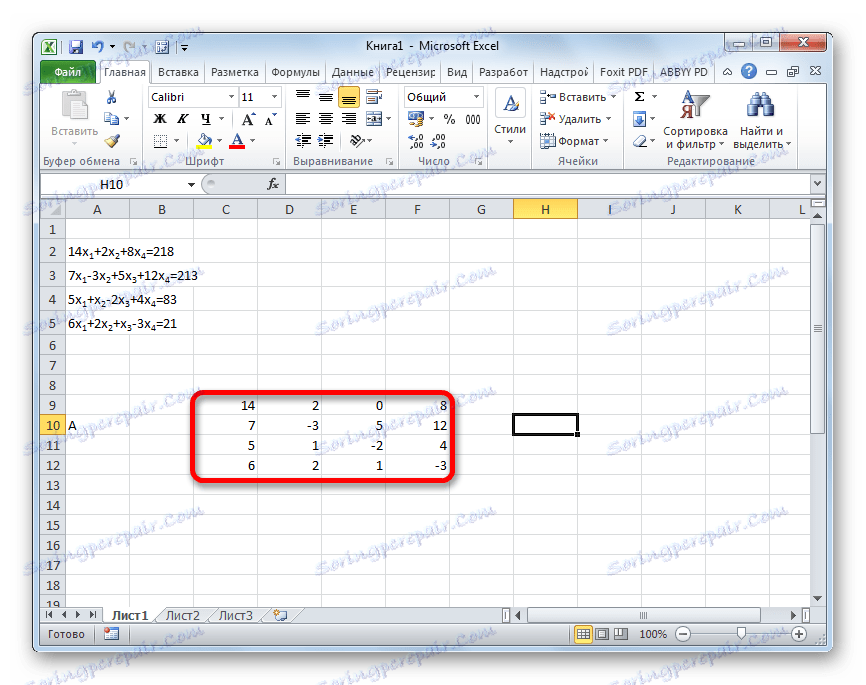
14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


1. Matrix vyplníme čísly, které jsou koeficienty rovnice. Tato čísla musí být uspořádána postupně, s ohledem na umístění každého kořene, ke kterému odpovídají. Pokud v jednom vyjádření chybí jeden kořen, potom se v tomto případě považuje koeficient za rovný nule. Pokud koeficient není uveden v rovnici, ale je přítomen odpovídající kořen, předpokládá se koeficient 1 . Označujeme výslednou tabulku jako vektor A.
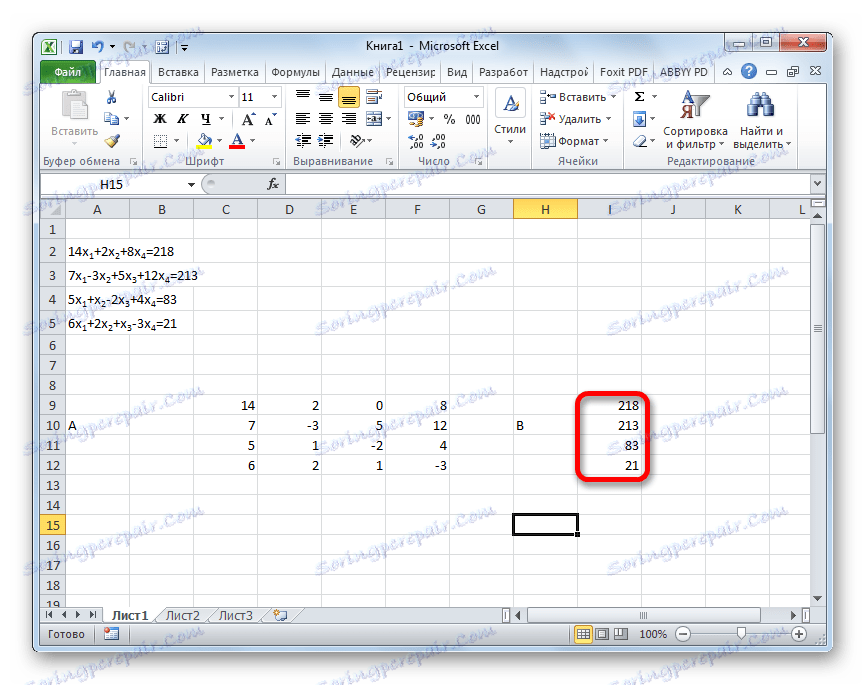
2. Samostatně zapište hodnoty za znaménko "se rovná". Označte je jejich společným jménem jako vektor B.
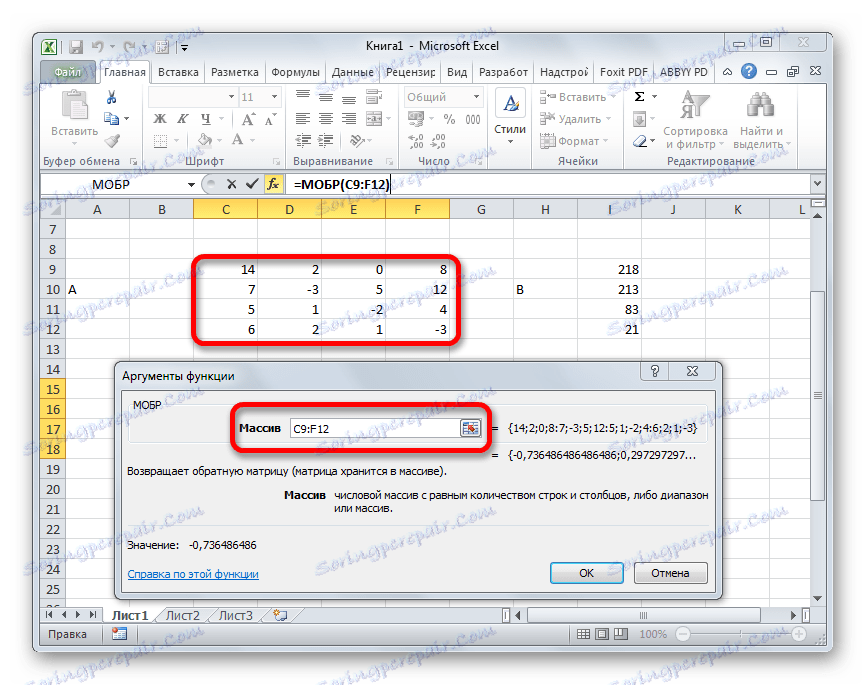
3. Za prvé, abychom našli kořeny rovnice, musíme najít inverzní matici stávající rovnice. Naštěstí má aplikace Excel zvláštní operátor, který je určen k vyřešení tohoto problému. Říká se tomu ICBM . Má poměrně jednoduchou syntaxi:

   =МОБР(массив)

   Argument "Array" je ve skutečnosti adresa zdrojové tabulky.

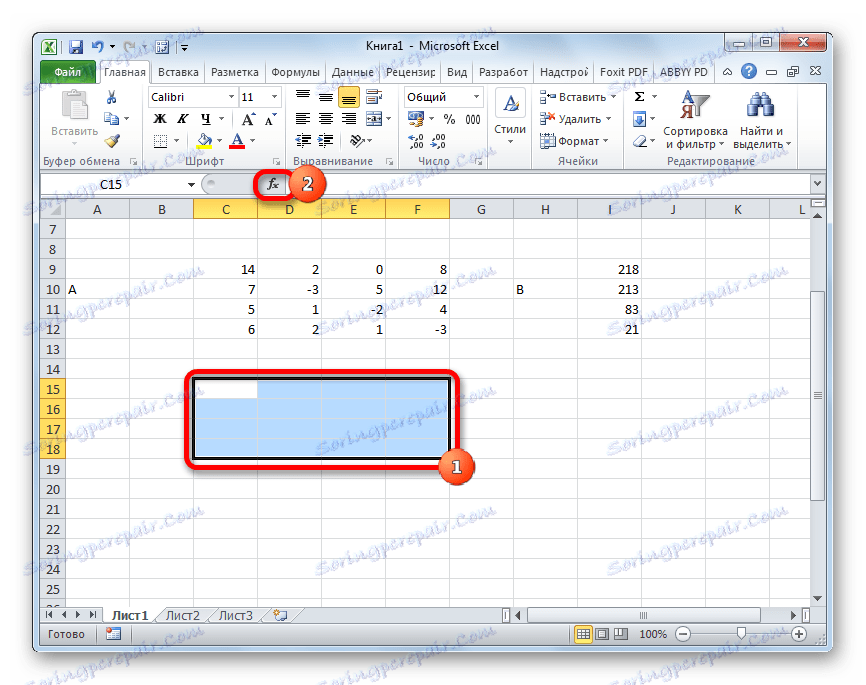
   Takže vybíráme oblast prázdných buněk na listu, která je stejná jako velikost původní matice. Klepněte na tlačítko "Vložit funkci" , který se nachází v blízkosti řádku vzorce.

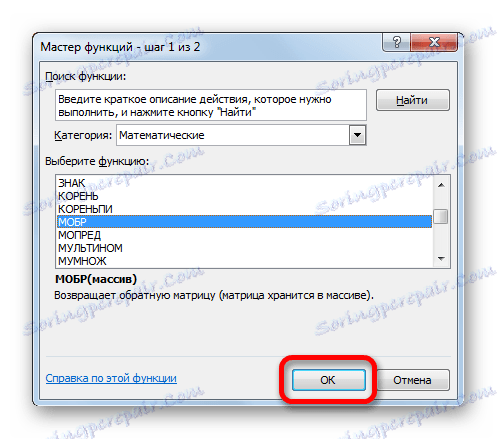
4. Spustí se Průvodce funkcí . Pojďme do kategorie "Matematické" . V prezentovaném seznamu hledáme název "MOBR" . Poté, co je nalezen, vyberte jej a klikněte na tlačítko "OK" .
5. Zobrazí se okno s argumenty funkce MOBR. Má pouze jedno pole v počtu argumentů - "Array" . Zde je třeba zadat adresu naší tabulky. Za tímto účelem nastavíme kurzor v tomto poli. Potom podržte levé tlačítko myši a vyberte oblast na listu, kde je matice umístěna. Jak vidíte, údaje o souřadnicích polohy se automaticky zadávají do pole okna. Po dokončení tohoto úkolu je nejzřetelnější kliknout na tlačítko "OK" , ale nepospíchejte. Faktem je, že klepnutí na toto tlačítko odpovídá použití příkazu Enter . Ale při práci s poli po dokončení zadání vzorce byste neměli klepnout na tlačítko Enter , ale vytvořit sadu klávesových zkratek Ctrl + Shift + Enter . Tuto operaci provádíme.
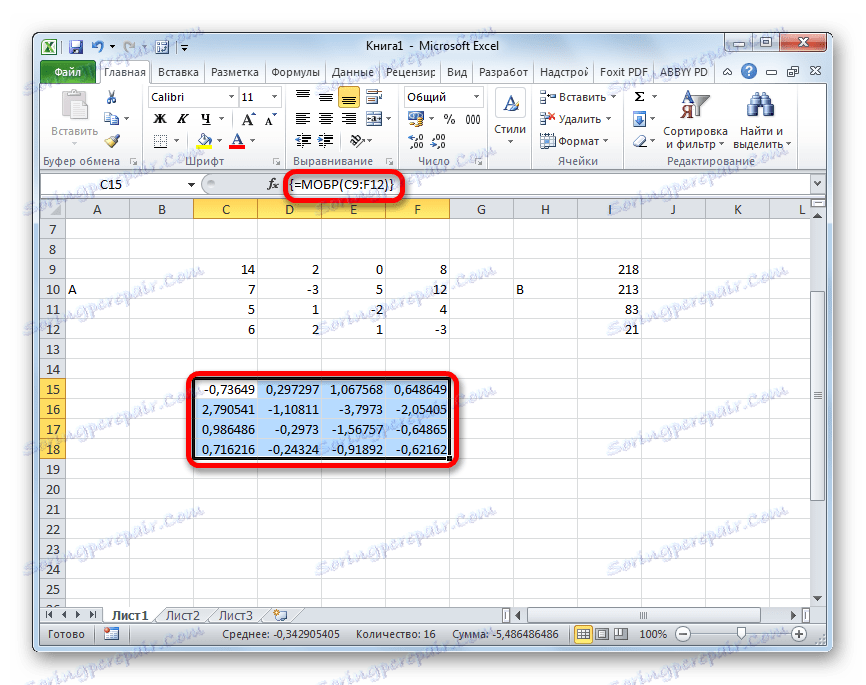
6. Takže po tomto programu program provádí výpočty a na výstupu v dříve přidělené oblasti máme matici, která je inversní.
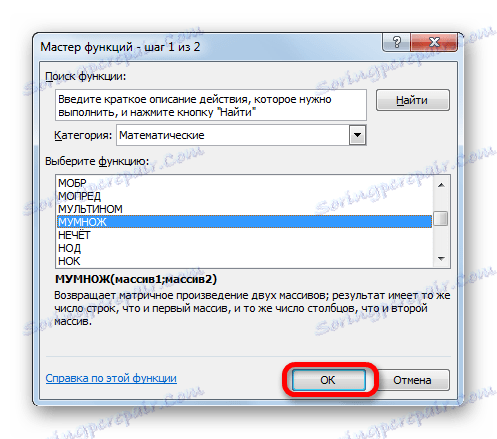
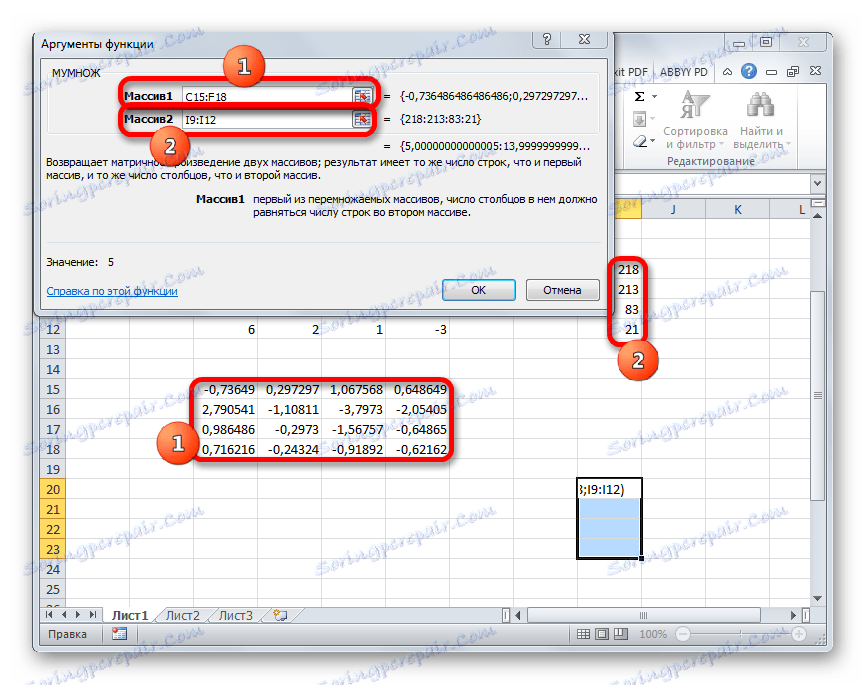
7. Nyní musíme inverzní matici vynásobit maticí B , která se skládá z jednoho sloupce hodnot umístěných za znaménkem rovnic ve výrazech. Pro násobení tabulek v aplikaci Excel existuje také samostatná funkce, která se nazývá HUMAN . Toto prohlášení má následující syntaxi:

   =МУМНОЖ(Массив1;Массив2)

   Vybíráme rozsah, v našem případě sestávající ze čtyř buněk. Spusťte Průvodce funkcí znovu kliknutím na ikonu "Vložit funkci" .

8. V kategorii "Matematická" , Průvodce začátkem funkcí vyberte název "HUMBLE" a klikněte na tlačítko "OK" .
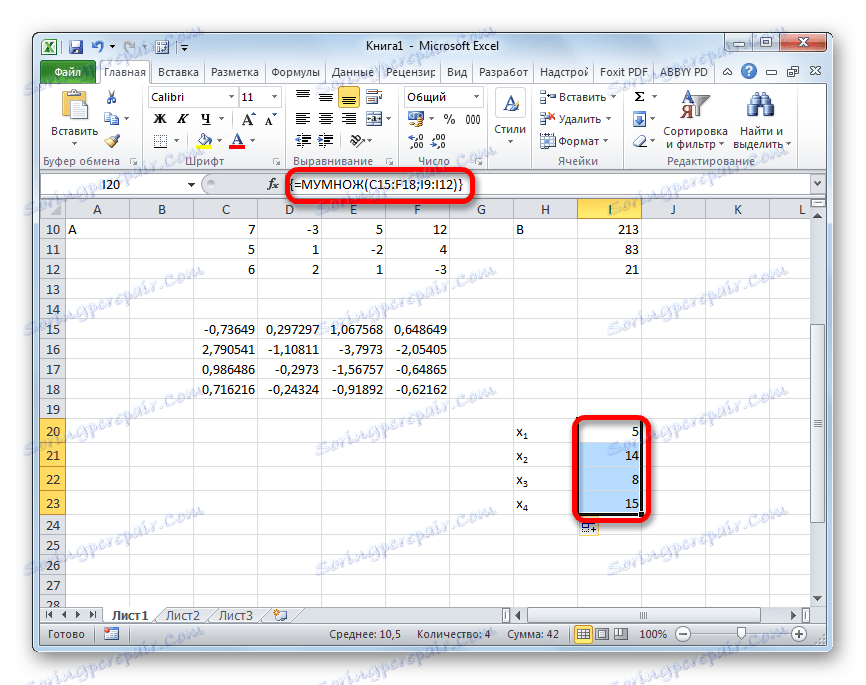
9. Okno argumentů funkce MULTI . V poli "Array1" zadáváme souřadnice naší inverzní matice. K tomu, stejně jako v poslední době, nastavíme kurzor v poli a levým tlačítkem myši zvolíme odpovídající tabulku s kurzorem. Provedeme podobnou akci pro zadání souřadnic v poli "Array2" , pouze tentokrát vybereme hodnoty sloupce B. Po provedení výše uvedených akcí opět nezapomeňte stisknout tlačítko "OK" nebo klávesu Enter a zadejte Ctrl + Shift + Enter .
10. Po této akci se kořeny rovnice zobrazují v předem vybrané buňce: X1 , X2 , X3 a X4 . Budou uspořádány postupně. Můžeme tedy říci, že jsme tento systém vyřešili. Aby bylo možné ověřit správnost řešení, stačí nahradit tyto kořeny původním systémem výrazů. Pokud je pozorována rovnost, znamená to, že prezentovaný systém rovnic je správně vyřešen.

Lekce: Inverzní matice v aplikaci Excel

Metoda 2: výběr parametrů

Druhou známou metodou řešení systému rovnic v aplikaci Excel je aplikace metody výběru parametrů. Podstata této metody spočívá v hledání opaku. To znamená, že na základě známého výsledku hledáme neznámý argument. Použijeme kvadratickou rovnici

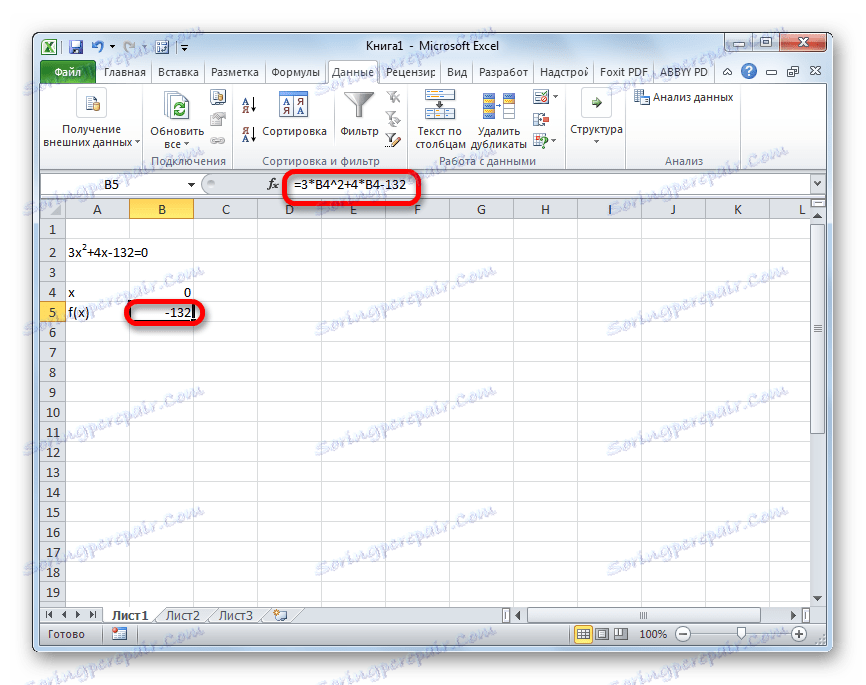
3x^2+4x-132=0

1. Předpokládejme, že hodnota x je rovna 0 . Vypočítáme odpovídající hodnotu f (x) použitím následujícího vzorce:

   =3*x^2+4*x-132

   Namísto hodnoty "X" nahraďte adresu buňky, kde je umístěno číslo 0 , které jsme použili pro x .

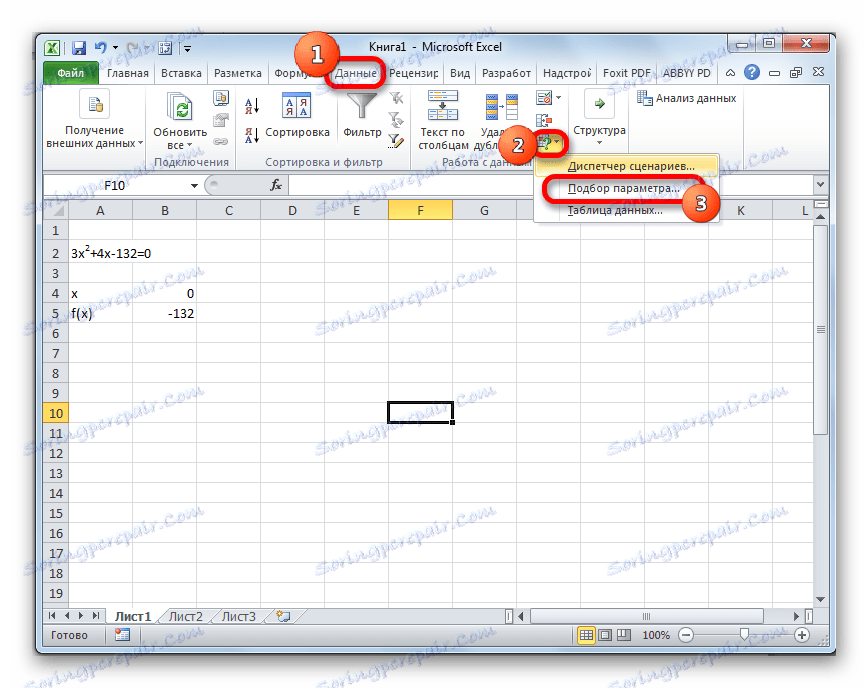
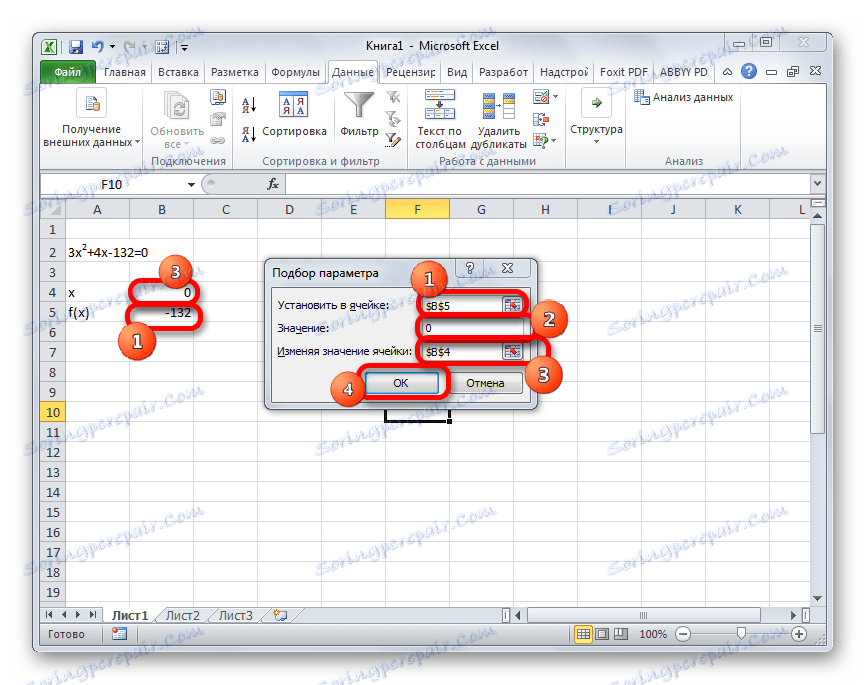
2. Přejděte na kartu "Data" . Klikněte na tlačítko "Analýza, co kdyby" . Toto tlačítko je umístěno na pásu v poli "Práce s daty" . Zobrazí se rozevírací seznam. Vyberte položku "Výběr parametrů ..." .
3. Otevře se okno pro výběr parametrů. Jak vidíte, skládá se ze tří polí. V poli "Nastavit v buňce" určíme adresu buňky, ve které je nalezen vzorec f (x) , který jsme vypočítali dříve. Do pole "Hodnota" zadejte číslo "0" . V poli "Změna hodnot" uveďte adresu buňky, ve které je umístěna hodnota x , která byla dříve použita pro hodnotu 0 . Po dokončení těchto kroků klikněte na tlačítko "OK" .
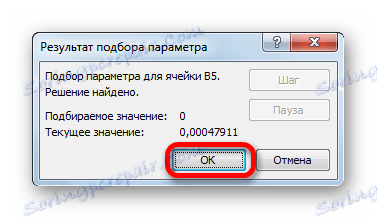
4. Poté Excel provede výpočet výběrem parametru. To se zobrazí v informačním okně, které se objevilo. V něm klikněte na tlačítko "OK" .
5. Výsledek výpočtu kořene rovnice bude v buňce, kterou jsme přiřadili do pole "Změna hodnot" . V našem případě, jak vidíme, x bude rovno 6 .

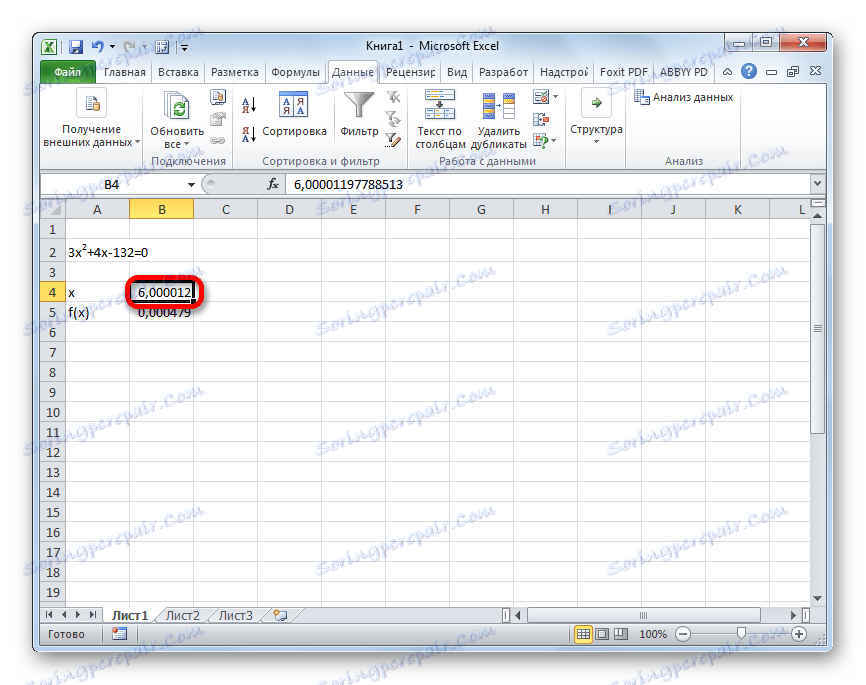
Tento výsledek lze také zkontrolovat nahrazením této hodnoty do vyřešeného výrazu namísto hodnoty x .

Lekce: Výběr parametrů v aplikaci Excel

Metoda 3: Cramerova metoda

Nyní se pokusíme vyřešit systém rovnic Cramerovou metodou. Používejte například stejný systém, který byl použit v režimu 1 :


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


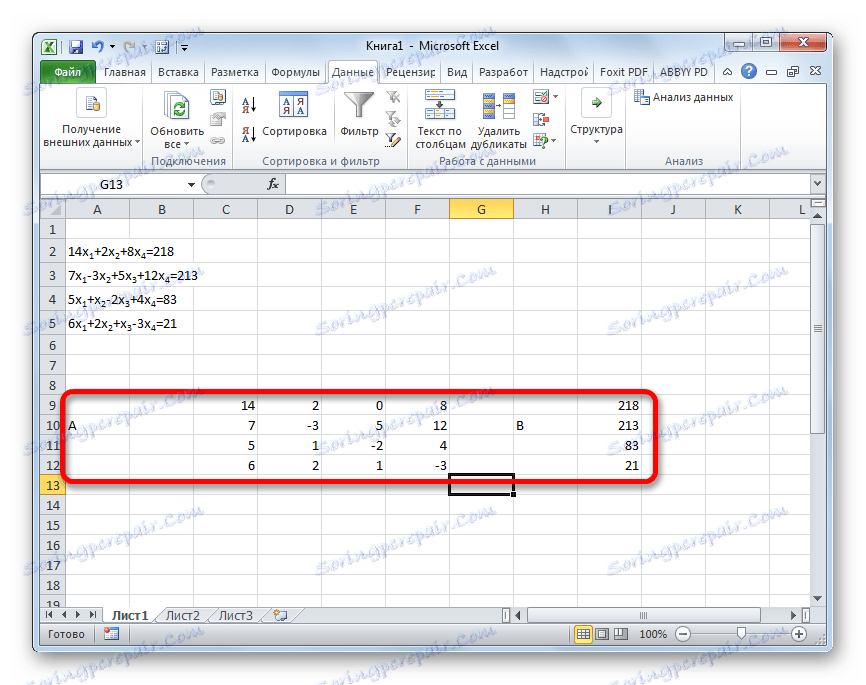
1. Stejně jako v první metodě sestavujeme matici A z koeficientů rovnic a tabulky B z hodnot, které se nacházejí za znaménkem "rovný" .
2. Pak uděláme další čtyři tabulky. Každá z nich je kopií matice A , pouze pro tyto kopie je jeden sloupec nahrazen tabulkou B střídavě. První tabulka má první sloupec, druhá tabulka má druhý sloupec a tak dále.
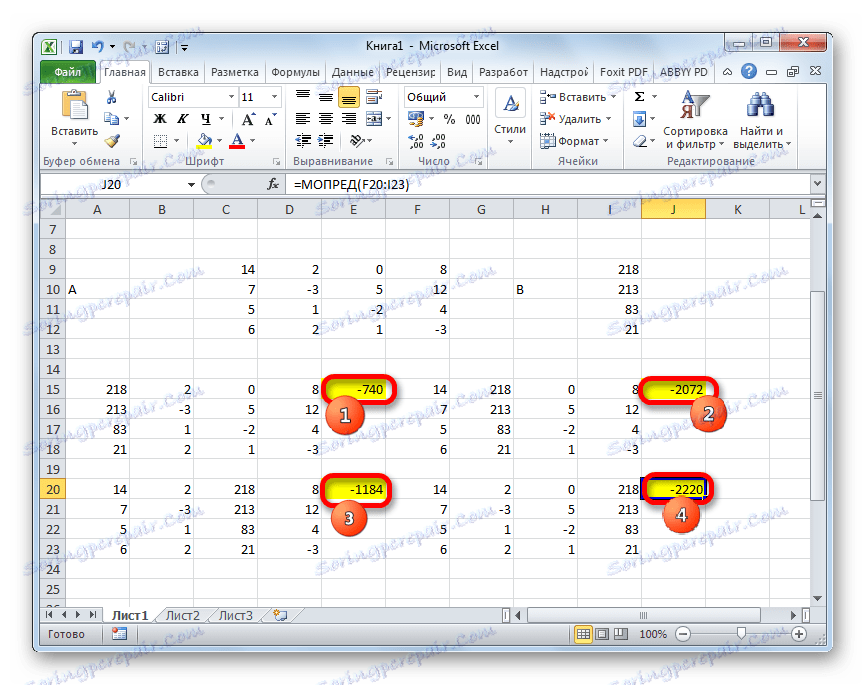
3. Teď potřebujeme vypočítat determinanty pro všechny tyto tabulky. Systém rovnic bude mít řešení pouze tehdy, pokud mají všechny determinanty hodnotu odlišnou od nuly. Chcete-li znovu vypočítat tuto hodnotu v aplikaci Excel, existuje samostatná funkce - MOPRED . Syntaxe tohoto operátora je:

   =МОПРЕД(массив)

   Tak jako v případě funkce MBD je jediným argumentem odkaz na zpracovanou tabulku.

   Vyberte buňku, ve které se bude zobrazovat determinant první matice. Potom klikněte na tlačítko "Vložit funkci" , které je známé z předchozích metod.

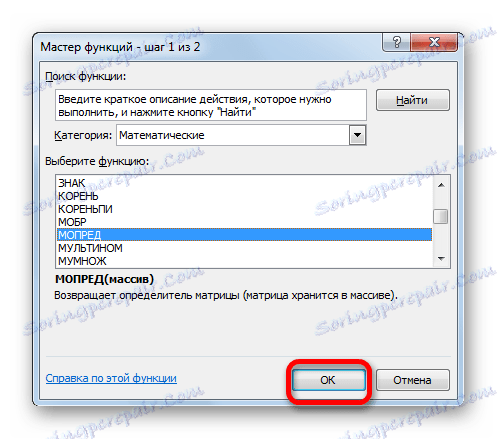
4. Okno Průvodce je aktivováno. Přecházíme do kategorie "Matematické" a mezi seznamem operátorů vybíráme tam název "MOPRED" . Poté klikněte na tlačítko "OK" .
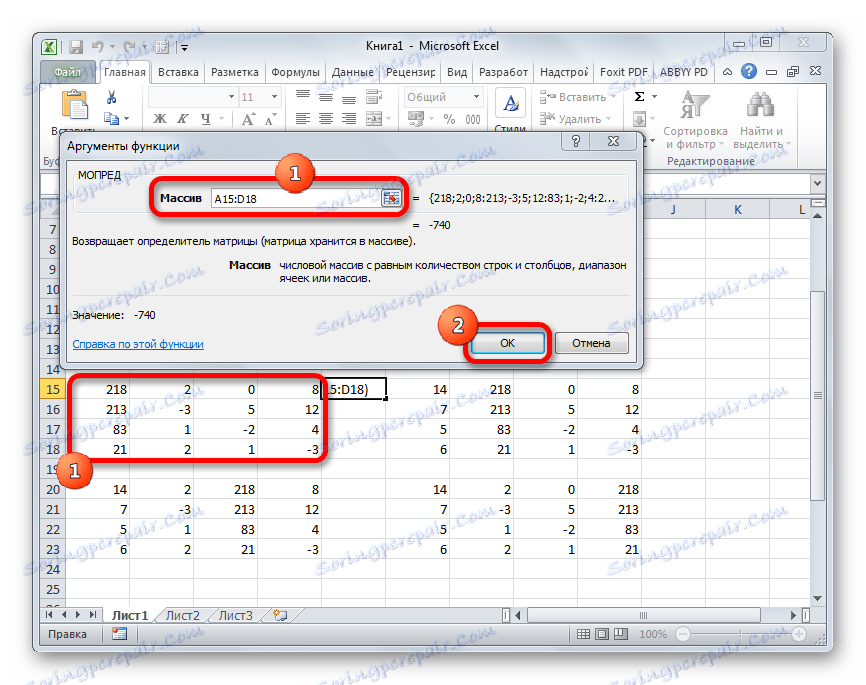
5. Otevře se okno argumentů funkce MOPED . Jak vidíte, má pouze jedno pole - "Array" . V tomto poli zadáváme adresu první transformované matice. Chcete-li to provést, nastavte kurzor v poli a vyberte oblast matice. Poté klikněte na tlačítko "OK" . Tato funkce zobrazuje výsledek v jedné buňce, nikoliv v poli, takže pro výpočet nemusíte stisknout klávesy Ctrl + Shift + Enter .
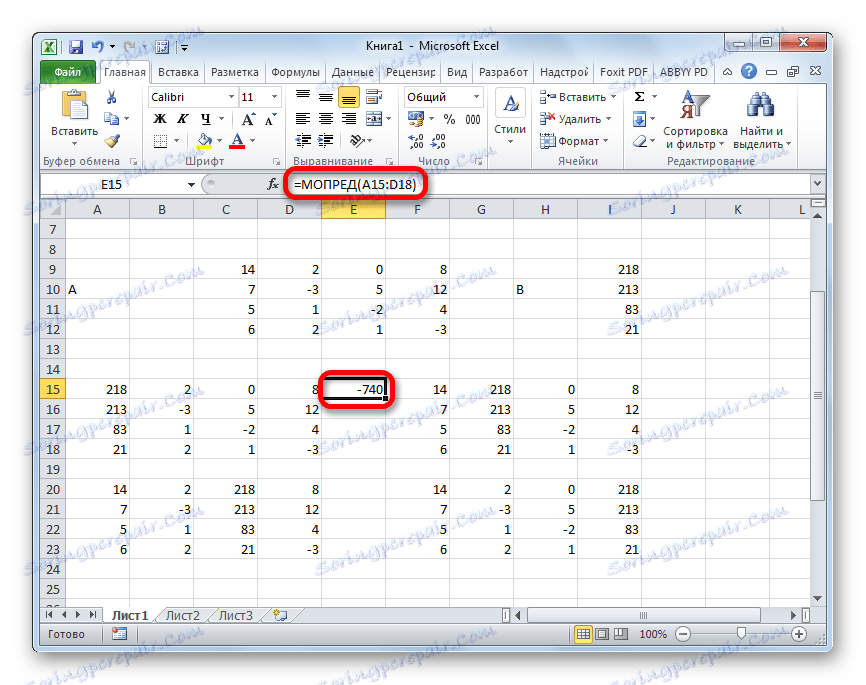
6. Funkce vypočítá výsledek a vyvede ji do předem vybrané buňky. Jak vidíte, v našem případě je determinantem -740 , to znamená, že není rovno nule, což je pro nás vhodné.
7. Podobně vypočítáme determinanty pro zbývající tři tabulky.
8. V závěrečné fázi vypočítáme determinant primární matice. Postup je stejný pro stejný algoritmus. Jak je vidět, determinant primární tabulky se také liší od nuly, a proto je matice považována za nedegenerovanou, tj. Systém rovnic má řešení.
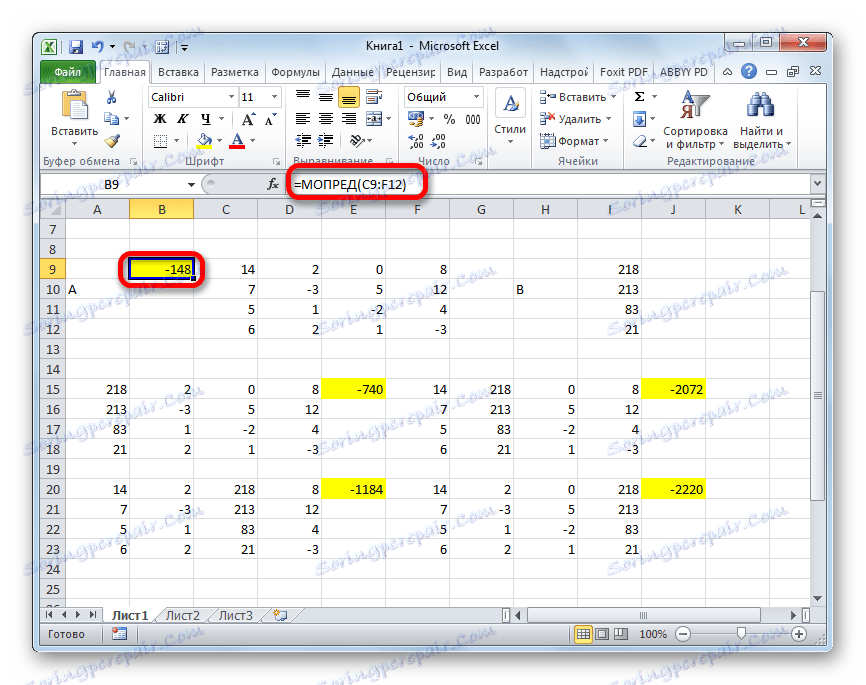
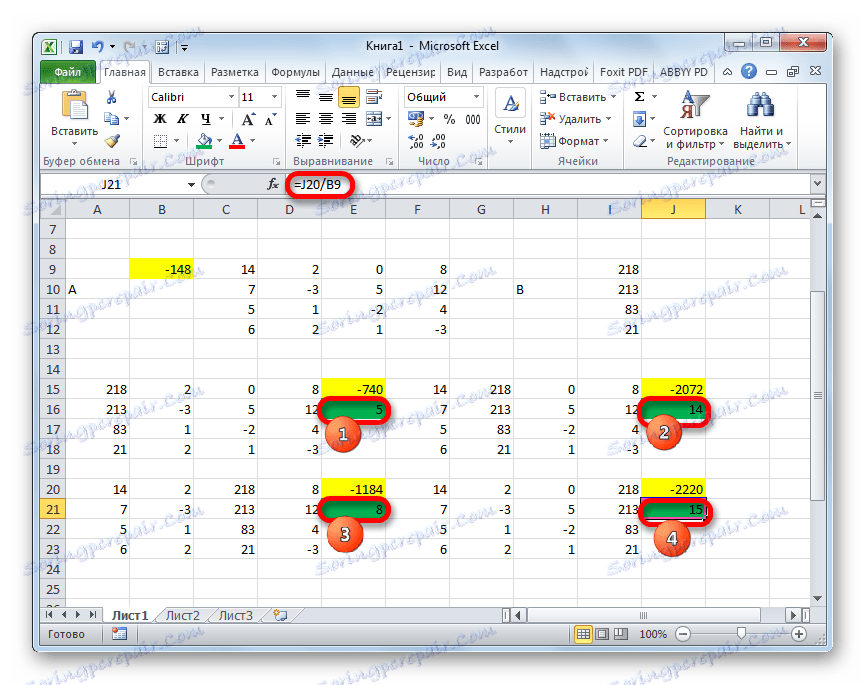
9. Nyní je čas najít kořeny rovnice. Kořen rovnice se bude rovnat poměru determinantu odpovídající transformované matice k determinantu primární tabulky. Takže po rozdělení všech čtyř determinantů transformovaných matic jeden po druhém -148 , což je determinant původní tabulky, získáme čtyři kořeny. Jak vidíte, jsou stejné jako hodnoty 5 , 14 , 8 a 15 . Proto se přesně shodují s kořeny, které jsme nalezli pomocí inverzní matice v metodě 1 , což potvrzuje správnost řešení systému rovnic.

Metoda 4: Gaussova metoda

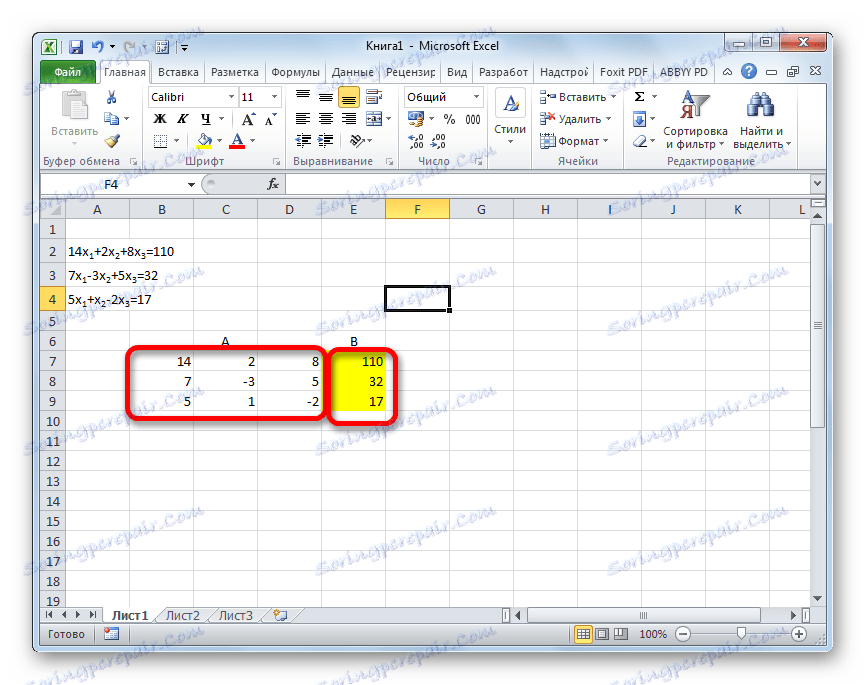
Řešení systému rovnic lze také provést pomocí Gaussovy metody. Například, vezměme si jednodušší systém rovnic tří neznámých:


14 x1 +2 x2 +8 x3 =110
7 x1 -3 x2 +5 x3 =32
5 x1 + x2 -2 x3 =17


1. Znovu zaznamenáváme postupně koeficienty v tabulce A a volné termíny umístěné za znaménkem "se rovná" v tabulce B. Tentokrát však přiblížíme obě tabulky, protože to bude nutné, abychom mohli v budoucnu pracovat. Důležitou podmínkou je, že v první buňce matice A je hodnota odlišná od nuly. V opačném případě byste měli řádky uspořádat na místech.
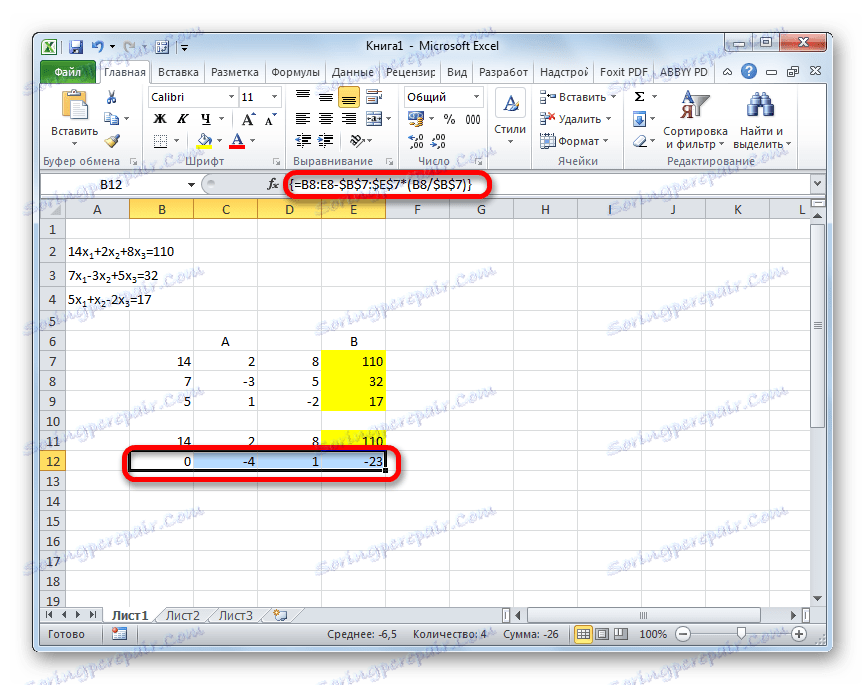
2. Zkopírujte první řádek dvou připojených matic do řádku níže (pro přehlednost můžete přeskočit jeden řádek). V první buňce, která se nachází v řádku ještě nižší než předchozí, zadejte následující vzorec:

   =B8:E8-$B$7:$E$7*(B8/$B$7)

   Pokud uspořádáte matice jinak, budou adresy buněk vzorce mít pro vás jinou hodnotu, ale můžete je vypočítat porovnáním s formulemi a obrázky, které jsou zde uvedeny.

   Po zadání vzorce vyberte celý řádek buněk a stiskněte klávesy Ctrl + Shift + Enter . Vzorec pole bude aplikován na řádek a bude vyplněn hodnotami. Tak jsme odečtení od druhého řádku první, násobený poměrem prvních koeficientů prvních dvou výrazů systému.

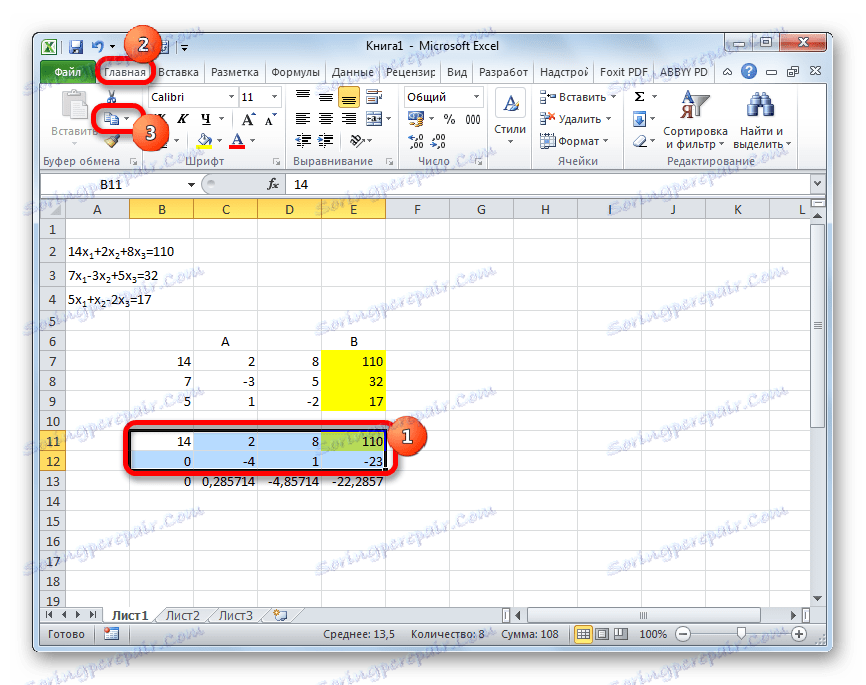
3. Poté zkopírujte výsledný řádek a vložte jej do řádku níže.
4. Vyberte první dva řádky za chybějící čárou. Klikněte na tlačítko "Kopírovat" , které se nachází na pásu karet na kartě Domů .
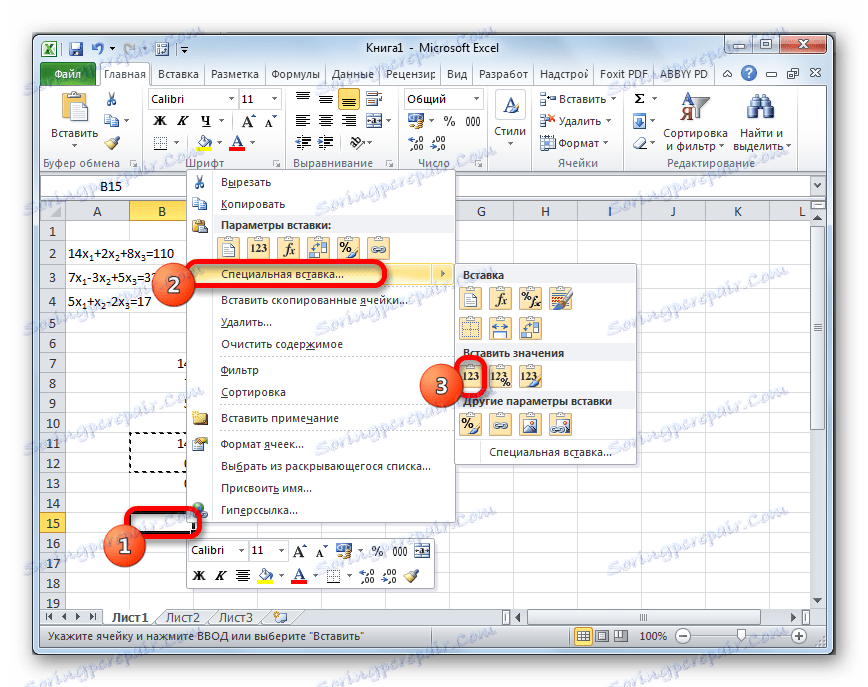
5. Přeskočíme linku po posledním záznamu na listu. Vyberte první buňku v dalším řádku. Klikněte pravým tlačítkem myši. V otevřené kontextové nabídce umístíme kurzor nad položku "Zvláštní vložit" . V dalším seznamu, který se spustí, vyberte položku "Hodnoty" .
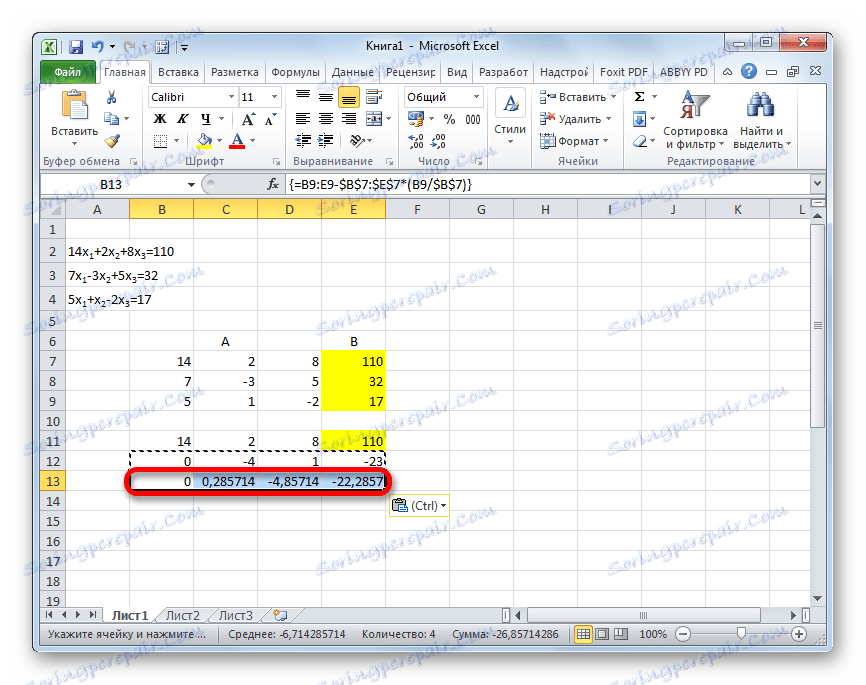
6. V dalším řádku zadejte vzorec pole. Odpočítává druhý řádek od třetího řádku předchozí skupiny dat vynásobený poměrem druhého koeficientu třetího a druhého řádku. V našem případě bude mít vzorec následující formu:

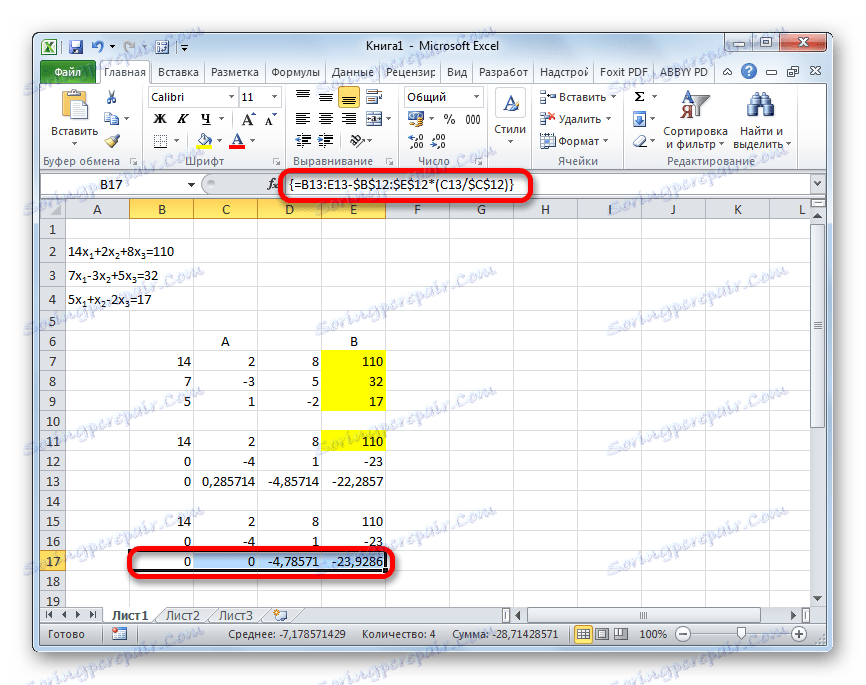
   =B13:E13-$B$12:$E$12*(C13/$C$12)

   Po zadání vzorce použijte celou řadu a použijte klávesové zkratky Ctrl + Shift + Enter .

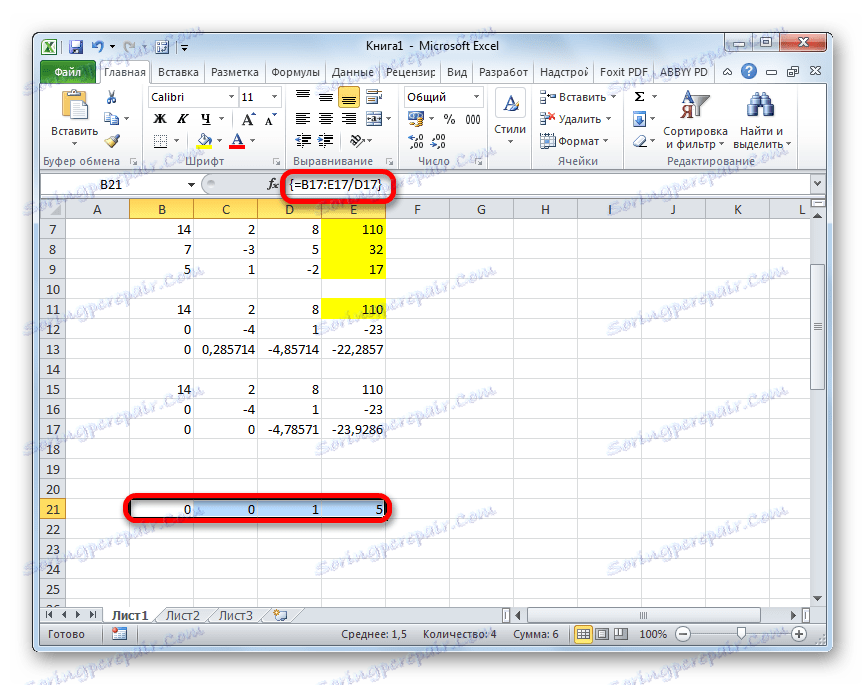
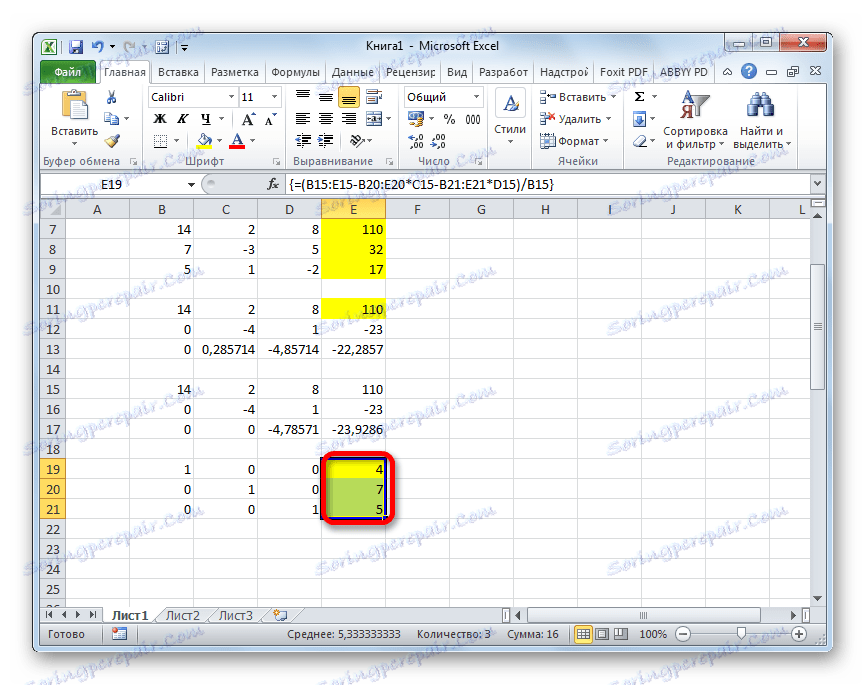
7. Nyní je nutné provést zpětný chod pomocí Gaussovy metody. Přeskočíme tři řádky z posledního záznamu. Ve čtvrtém řádku zadáváme vzorec pole:

   =B17:E17/D17

   Dělíme tedy poslední řádek, který jsme vypočítali podle třetího koeficientu. Po zadání vzorce vyberte celý řádek a stiskněte klávesy Ctrl + Shift + Enter .

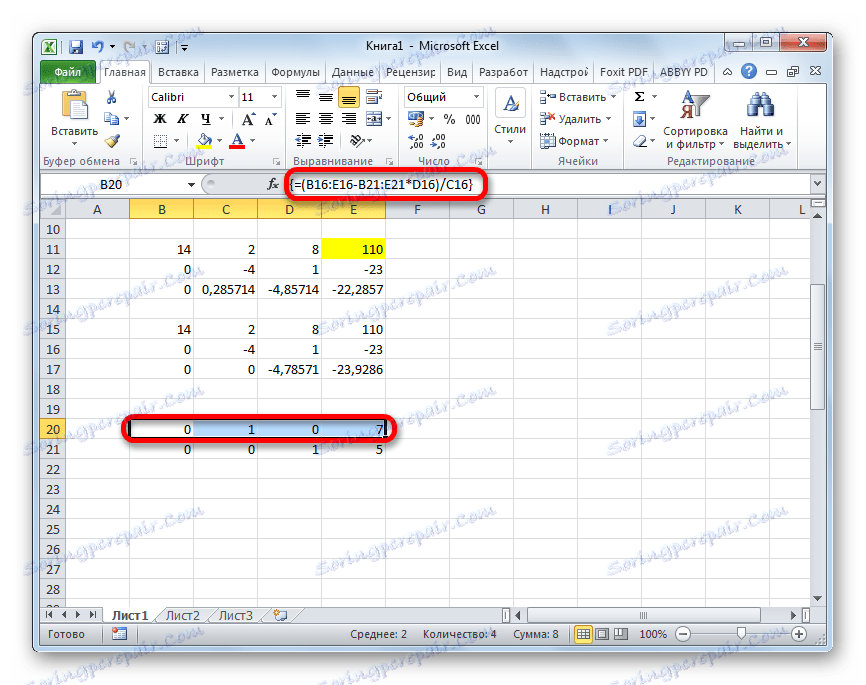
8. Stoupáme na řádek vzhůru a vstoupíme do ní následující vzorec pole:

   =(B16:E16-B21:E21*D16)/C16

   Stiskneme obvyklou kombinaci kláves, která použije vzorec pole.

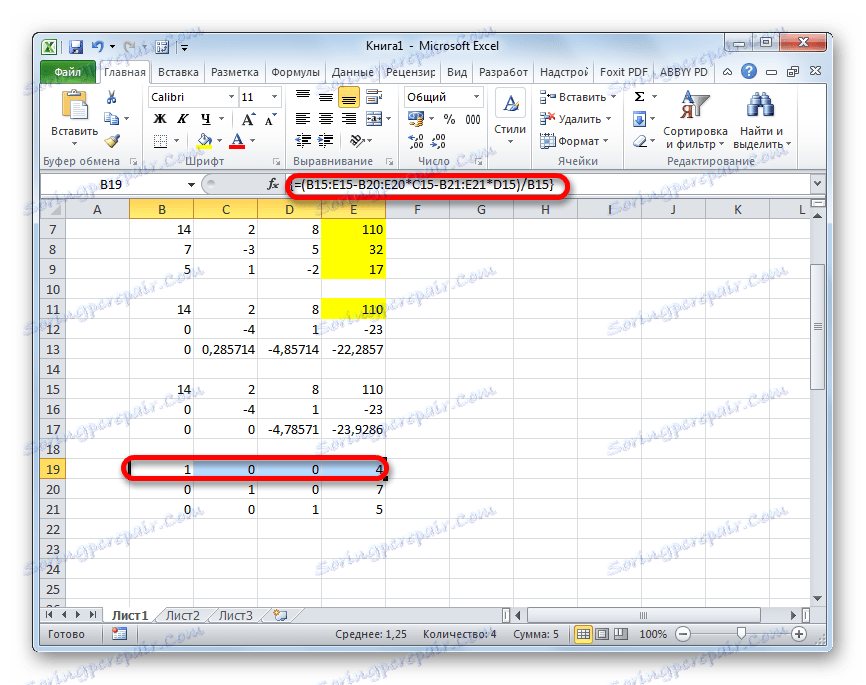
9. Stoupáme ještě o jednu řadu výše. V něm zadejte vzorec pole v následujícím tvaru:

   =(B15:E15-B20:E20*C15-B21:E21*D15)/B15

   Znovu vyberte celý řádek a použijte kombinaci kláves Ctrl + Shift + Enter .

10. Nyní se podívejme na čísla, která byla získána v posledním sloupci posledního bloku řádků, který jsme předem vypočítali. Právě tato čísla ( 4 , 7 a 5 ) budou kořeny daného systému rovnic. Můžete to zkontrolovat nahrazením namísto X1 , X2 a X3 ve výrazech.

Jak je vidět, v systému Excel může být systém rovnic řešen řadou metod, z nichž každá má své vlastní výhody a nevýhody. Všechny tyto metody však mohou být podmíněně rozděleny do dvou velkých skupin: matice a pomocí nástroje pro výběr parametrů. V některých případech nejsou vhodné pro řešení problému vždy matricové metody. Konkrétně, když je determinant matice nulový. V ostatních případech se uživatel může rozhodnout, jakou volbu považuje za výhodnější pro sebe.

• ← Vytváření paraboly v aplikaci Microsoft Excel
• Vytvoření tlačítka v aplikaci Microsoft Excel →