Excel

Pomocí analýzy clusterů v aplikaci Microsoft Excel

Jedním z nástrojů pro řešení ekonomických problémů je analýza klastrů. Pomocí této skupiny se seskupí a další objekty v řadě dat rozdělí do skupin. Tuto metodu lze použít v aplikaci Excel. Uvidíme, jak se to děje v praxi.

Pomocí analýzy klastrů

Pomocí analýzy klastrů je možné vzorek na základě toho, co se zkoumá. Jeho hlavním úkolem je rozdělit vícerozměrné pole do homogenních skupin. Jako kritérium seskupení se podle daného parametru použije korelační koeficient pár nebo euklidovská vzdálenost mezi objekty. Nejbližší hodnoty jsou vzájemně seskupeny.

Ačkoli se nejčastěji používá tento typ analýzy v ekonomice, může být také použit v biologii (pro klasifikaci zvířat), psychologii, medicíně a v mnoha dalších oblastech lidské činnosti. Klastrová analýza může být použita za použití standardního toolkitu Excel.

Příklad použití

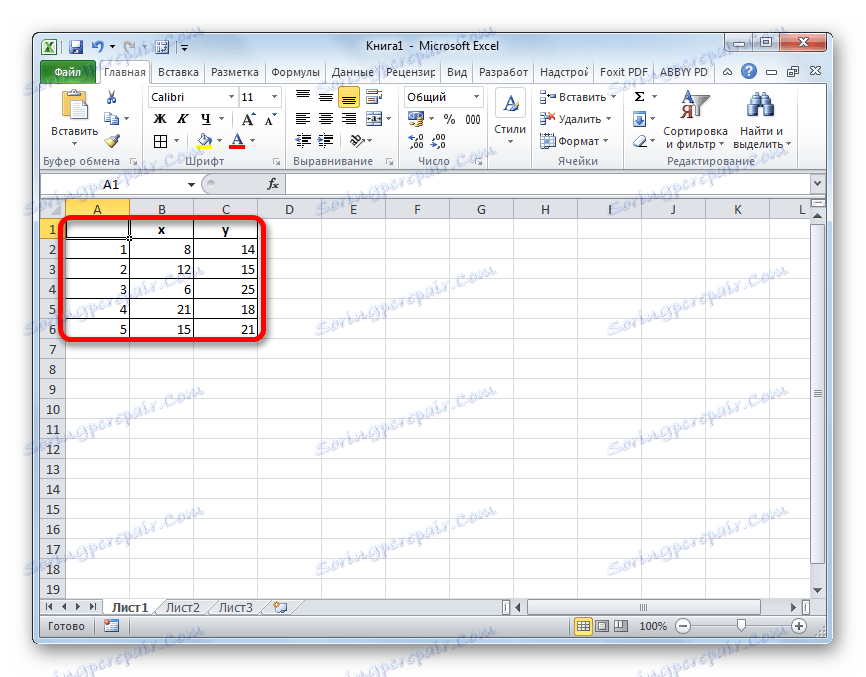
Máme pět objektů, které jsou charakterizovány dvěma sledovanými parametry - x a y .

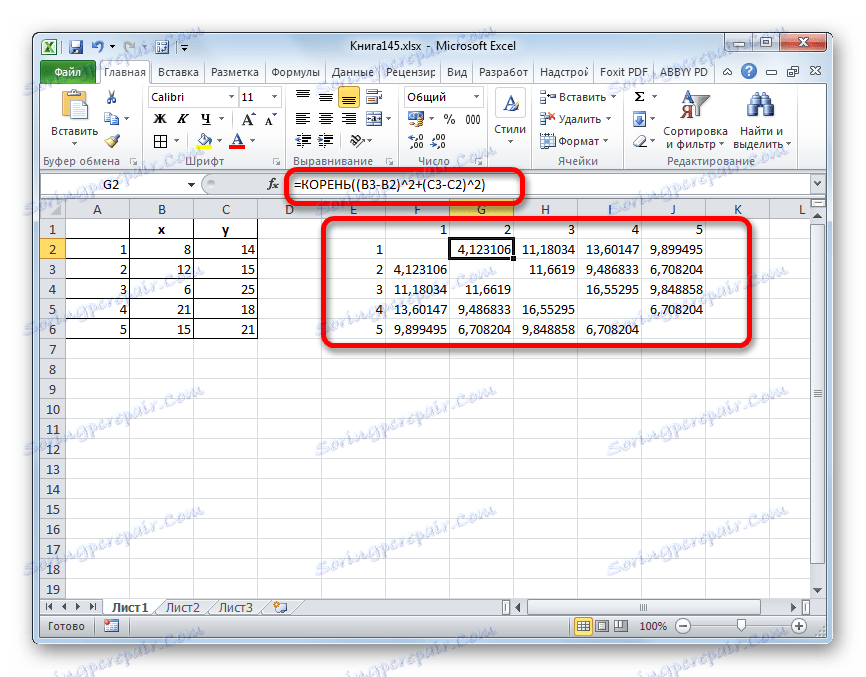
  1. Na tyto hodnoty aplikujte vzorec euklidovské vzdálenosti, která je vypočítána z šablony:

    =КОРЕНЬ((x2-x1)^2+(y2-y1)^2)

    2. Naučené objekty v aplikaci Microsoft Excel

  2. Tato hodnota se vypočítá mezi každým z pěti objektů. Výsledky výpočtu jsou umístěny v matici vzdáleností.

    3. Vzdálenost matice v aplikaci Microsoft Excel

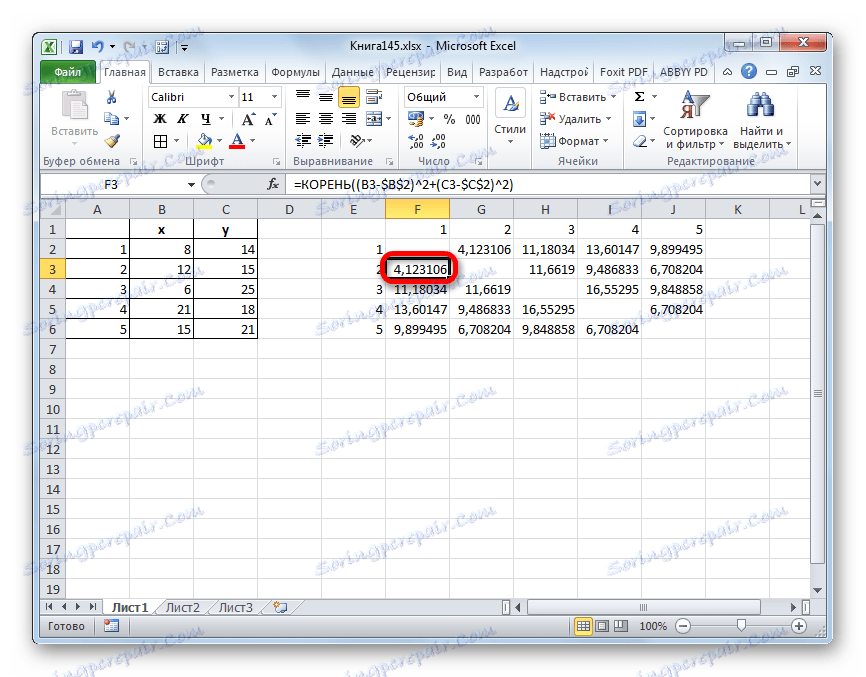
  3. Podíváme se, mezi kterými hodnotami je nejmenší vzdálenost. V našem příkladu jsou to objekty 1 a 2 . Vzdálenost mezi nimi je 4.123106, což je méně než mezi jinými prvky dané populace.

    4. Vzdálenost mezi objekty je v aplikaci Microsoft Excel minimální

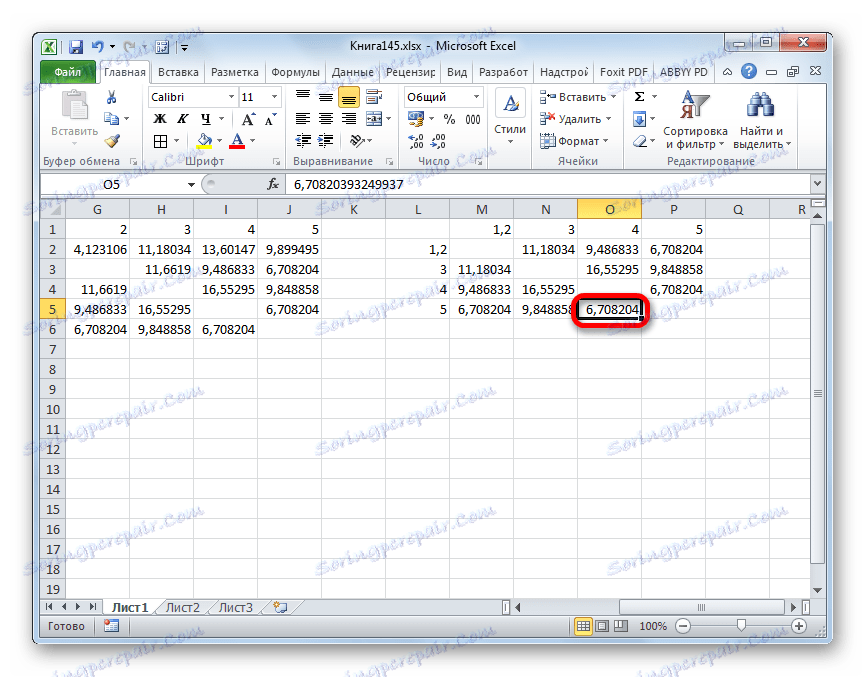
  4. Kombinujeme tyto údaje do skupiny a tvoříme novou matici, ve které hodnoty 1,2 jsou samostatným prvkem. Při sestavování matice opustíme nejmenší hodnoty z předchozí tabulky pro kombinovaný prvek. Znovu se podíváme, mezi kterými prvky je vzdálenost minimální. Tentokrát to je 4 a 5 , a také objekt 5 a skupina objektů 1,2 . Vzdálenost je 6,708204.

    5. Vzdálenost mezi objekty je minimální v druhé matici v aplikaci Microsoft Excel

  5. Přidáme specifikované prvky do obecného clusteru. Vytvoříme novou matici stejného principu jako v předchozím čase. To znamená, že hledáme nejnižší hodnoty. Takže vidíme, že náš datový soubor lze rozdělit na dva klastry. V prvním clusteru jsou nejbližší prvky 1 , 2 , 4 , 5 . Ve druhém seskupení je v našem případě zastoupen pouze jeden prvek - 3 . Je poměrně daleko od jiných objektů. Vzdálenost mezi klastry je 9,84.

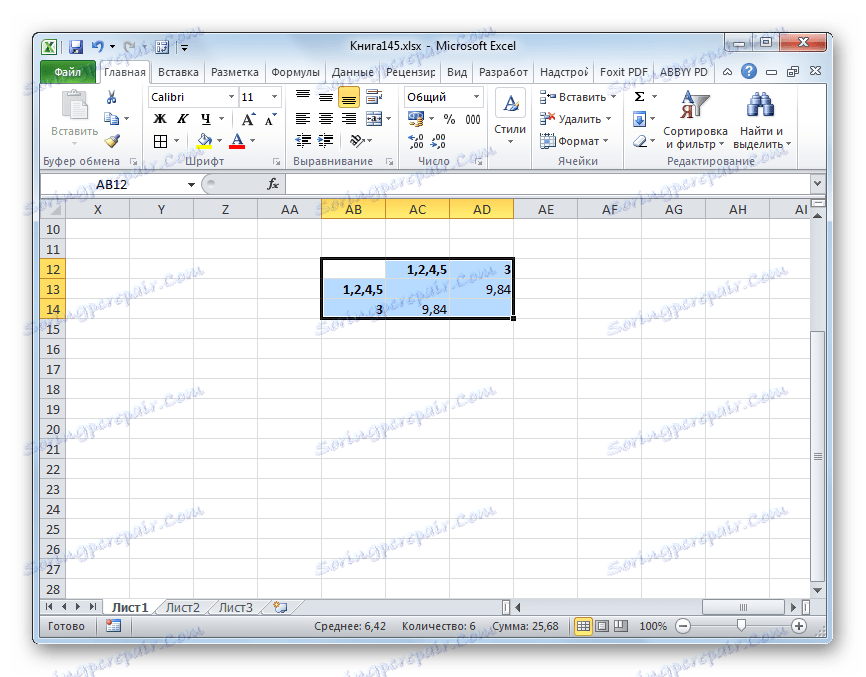
Celková hodnota v aplikaci Microsoft Excel

Tím se uzavírá postup pro rozdělení sbírky do skupin.

Jak je vidět, ačkoli obecně se klastrová analýza může zdát komplikovaným postupem, není tak obtížné pochopit nuance této metody. Hlavní věc je pochopit základní strukturu seskupení.